Prawidłowość
miłosz:
Wyznaczyć:
B/A
A=(1;5), B(2;6>
Czy to będzie− B/A= (1;2) ,(5;6>

10 sie 19:26
picia:
nie

10 sie 19:28
picia:
a co oznacza przecinek?
10 sie 19:28
picia:
B/A wszystko co jest w B a nie ma w A
10 sie 19:29
miłosz: sorry
10 sie 19:30
miłosz: źle zrobiłem
10 sie 19:30
miłosz: Wyznaczyć:
B/A
A=(1;5), B(2;6>
B/A= (5;6> ,dobrze

10 sie 19:31
Basia:
narysuj to miłosz
B − czerwonym; A − niebieskim
szukasz B\A zasłoń niebieskie i zobacz co zostanie
uważaj na końce przedziałów
10 sie 19:32
Basia: nie do końca dobrze
B\A = <5;6>
bo 5 nie należy do A, czyli liczby 5 nie "wyrzucasz" z B
10 sie 19:33
Ja:
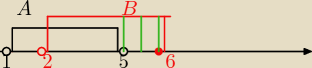
10 sie 19:35
miłosz:
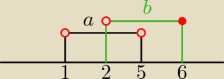
I tu jest moje pytanie, gdy usunąłem zbiór a ,to został kawałek b z zamalowanym kołkiem, i jak
to wtedy zapisać, czy (5;6> czy <5;6>

10 sie 19:37
Eta* :
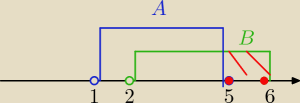 B\A
B\A=......
10 sie 19:37
picia:
5− jest w B a nie ma w A
10 sie 19:38
miłosz: Czyli co te znaki znaczą w zbiorach "<", " ) "

10 sie 19:40
Basia:
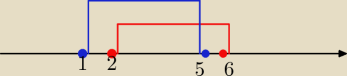
inny sposób rysowania
1, 5 ∉A dlatego kropki są na zewnątrz
2∉B dlatego kropka jest na zewnątrz
6∊B dlatego kropka jest wewnątrz
i teraz odrzucam A, ta kropka oznaczająca 5 mi zostaje
czyli mam B\A = <5;6>
10 sie 19:40
Basia: wrrrrrrrrrrrrrrrrrrrrrrr

10 sie 19:41
Eta* :

10 sie 19:41
Basia:
( ) przedział otwarty; końce do niego nie należą
< > przedział domknięty (zamknięty); końce do niego należą
10 sie 19:42
picia:
Miłosz juz Ci to pisalem.
<5 piatka jest w zbiorze
(5 tej piatki nie ma zbiorze (zbior jest od piatki ale bez niej)
10 sie 19:42
miłosz: dobre dobre nawet
10 sie 19:46
Eta* :
Takie dobre, jak


10 sie 19:47
picia:
zrób jakiś inny przyklad

10 sie 19:52
Eta* :
@miłosz
A= <−3, 2) B= (−1, 4>
AUB=...
A∩ B=..
A\B=..
B\A=...
10 sie 19:55
miłosz: Mam taki przykład i nie mogę tego narysować i odczytać prawidłowo tą Twoją metodą z kropkami:
A=(−∞;2>, B= <2;∞) ,pomóż
10 sie 20:03
miłosz: Chyba rozumiem już to
10 sie 20:05
picia:
to ile bedzie A∩B?
10 sie 20:06
Eta* :
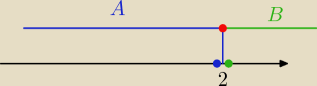
To prosty przykład,bo : A U B= R
A∩B=...
A\ B= ....
B\A=....
10 sie 20:08
miłosz: {2}
10 sie 20:08
Eta* :

10 sie 20:09
miłosz: A= <−3, 2) B= (−1, 4>
AUB= <−3;4>
A∩ B=(−1;2)
A\B=<−3;−1)
B\A=(2;4>
Dobrze

?
10 sie 20:10
picia:
dobrze, zrób teraz polecenie
Ety* 
10 sie 20:10
Basia:

tam "w środku" jest tylko liczba 2
stąd:
A∪B = (−
∞;+
∞) = R
A∩B = {2}
A\B = (−
∞; 2)
B\A = (2; +
∞)
10 sie 20:11
miłosz: A=(−∞;2>, B= (2;∞) zmieniłem w drugim znak na otwarty,
A∩B
to by był zbiór pusty ,prawda?
10 sie 20:11
picia:
prawda
10 sie 20:13
picia:
tam wyzej masz źle
10 sie 20:15
Basia:
wtedy A\B też będzie inne; pomyśl jakie
10 sie 20:18
picia:
ojejejejej
to zadanie A= <−3, 2) B= (−1, 4>
róznice zbiorow masz źle
10 sie 20:20
miłosz: To jest dobrze , jak niby ma to wyglądać , te różnice

10 sie 20:27
miłosz: podbijam!
10 sie 20:31
picia:
juz pisze
10 sie 20:36
picia:
A/B= <−3; −1>
B/A= <2;4>
10 sie 20:37
miłosz: Tak to powinno wyglądać

10 sie 20:42
miłosz: jak napisałaś?
10 sie 20:42
miłosz: łeś ,raczej
10 sie 20:43
picia:
A\B w A jest −1 a w B −1 nie ma
B\A w B jest 2 a w A nie ma 2
mowa o A= <−3, 2) B= (−1, 4>
10 sie 20:44
picia:
łeś, łeś

10 sie 20:48




 I tu jest moje pytanie, gdy usunąłem zbiór a ,to został kawałek b z zamalowanym kołkiem, i jak
to wtedy zapisać, czy (5;6> czy <5;6>
I tu jest moje pytanie, gdy usunąłem zbiór a ,to został kawałek b z zamalowanym kołkiem, i jak
to wtedy zapisać, czy (5;6> czy <5;6>
 B\A=......
B\A=......

 inny sposób rysowania
1, 5 ∉A dlatego kropki są na zewnątrz
2∉B dlatego kropka jest na zewnątrz
6∊B dlatego kropka jest wewnątrz
i teraz odrzucam A, ta kropka oznaczająca 5 mi zostaje
czyli mam B\A = <5;6>
inny sposób rysowania
1, 5 ∉A dlatego kropki są na zewnątrz
2∉B dlatego kropka jest na zewnątrz
6∊B dlatego kropka jest wewnątrz
i teraz odrzucam A, ta kropka oznaczająca 5 mi zostaje
czyli mam B\A = <5;6>





 To prosty przykład,bo : A U B= R
A∩B=...
A\ B= ....
B\A=....
To prosty przykład,bo : A U B= R
A∩B=...
A\ B= ....
B\A=....

 ?
?

 tam "w środku" jest tylko liczba 2
stąd:
A∪B = (−∞;+∞) = R
A∩B = {2}
A\B = (−∞; 2)
B\A = (2; +∞)
tam "w środku" jest tylko liczba 2
stąd:
A∪B = (−∞;+∞) = R
A∩B = {2}
A\B = (−∞; 2)
B\A = (2; +∞)


